[kaggle Course] Notes

Posted on Disqus:

ML

流程

  • 匯入需要的module ，檔案
1
2
3
import pandas as pd 
file_path =  '../input/data/melb_data.csv'
home_data = pd.read_csv(file_path)

  • 選定要分析的 response y 和 features X

    1
    2
    3
    y= home_data.prices
    melb_features = ['Rooms', 'Bathroom', 'Landsize', 'Lattitude', 'Longtitude']
    X = home_data[melb_features]

  • 有些還會需要將原有資料做split。
    將資料分成training和verify data (通常為 80% : 20%)

  • 建立所需的模型
    看是要利用哪一種迴歸模型(目前有看到的Random forest, desicion tree regressor)

1
2
3
4
graph LR
A[Estimator的主要兩個方法] --> B[fit]
A --> C[Transform]

1
2
3
4
import sklearn.tree import DescisionTreeRegressor

melb_model = DecisionTreeRegressor(random_state= 1)
melb_model.fit(X,y)

  • 利用模型進行預測 

    1
    2
    3
    # compare the origin data and prediction data 
    print(X.head())
    print(melb_model.predict(X.head()))

  • 模型驗證(model validation)

    模型所預測的結果與實際發生的結果相近程度

但要用什麼方法來做驗證? metrics 矩陣
MAE (Mean absolute Error)
一般而言誤差指的是

error = actual - predicted
$$
MAE = 1/n \sum |y_{true} - y_{pred}|
$$

而在MAE 矩陣中, 我們將這個誤差轉換成一個正數
用來理解模型預測的品質
而這個數值可以理解成模型所預測的結果偏離實際的距離

  • Validate data

    在模型建立的過程中, 就先把某些部份的資料排除, 作為後續用來驗證模型預測品質的資料組

1
2
3
4
5
6
7
8
9
10
from sklearn.model_selection import train_test_split

train_x,val_X,train_y,val_Y = train_test_split(X,y,random_state=1)
#定義模型
mymodel = DecisionTreeRegressor()
mymodel.fit(train_x,train_y)

# 把 validate data 丟給模型, 做預測
val_predicted = mymodel.predict(val_X) 
print(mean_absolute_err(val_Y,val_predicted))
  • underfitting vs. overfitting

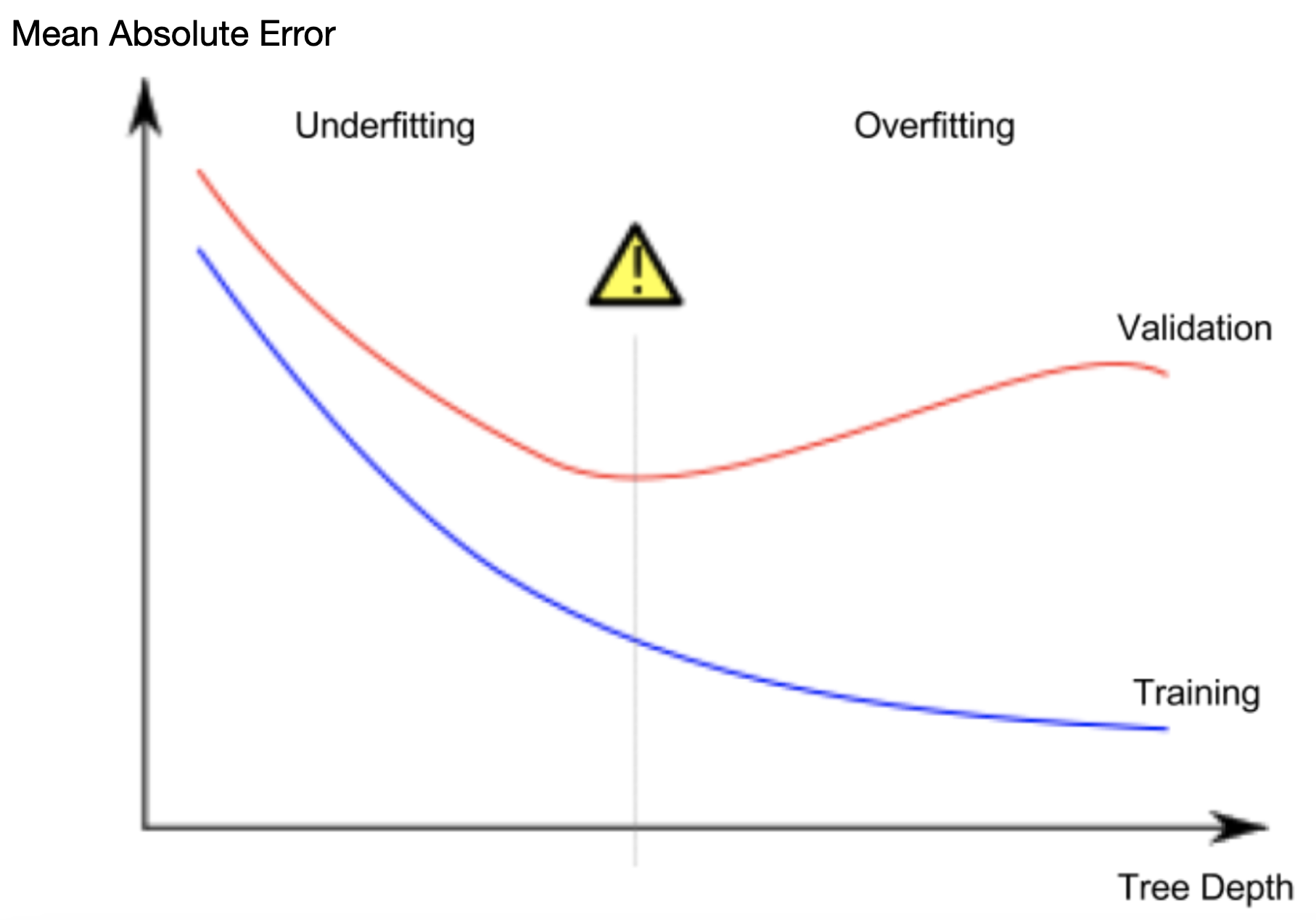
    • overfitting
      對模型現有的資料,可以擬合的狀態非常好, 但對於新的資料,卻並非總是如此

    • underfitting

對於決策樹的深度,不夠深, 造成不論是驗證的資料或是訓練資料都無法產生足夠好品質的預測結果

熵

用來量化資訊的不確定性。

Entropy : a qunatity from nformation theory to measure uncertainty
越多不確定性，越需要更多問題來做決策樹

  • Mutual Information(MI)
    MI 越小，表示兩個特徵的相關性越低。若為0，表示這兩個數值相互獨立。correlation 只能偵測線性的關係，mutual Information 可以偵測到任何形式的相關性。

Feature scaling

  1. Normalization : 把數值縮到[0，1]這個範圍
    $
    x_{norm}^{(i)} = \frac{x^{(i)} - x_{min}}{x_{max}-x_{min}}
    $

  2. Standardization : 把數值的平均值移到0，標準差移到1
    $
    x_{std}^{(i)} = \frac{x^{(i)} - \mu_x}{\sigma_x}
    $